도서 소개
반복이 중요한 건 알겠는데 어떻게 해야 효과적으로 반복할 수 있을까? <기적의 중학 도형>은 좌우뇌를 균형 있게 사용하여 더 쉽고, 더 효과적으로 반복할 수 있게 구성되어 있다. 기적의 계산법 연구회는 공부하는 방법을 몰라서 우왕좌왕하며 비효율적인 학습 방법에 좌절한 학생들이 쉽고 재미있게 수학을 정복할 수 있도록 가장 쉽고 가장 효과적인 반복학습을 설계했다.
출판사 리뷰
1. 중학수학, 왜 어려운가? 초등학교 때까지 수학을 잘하던 학생들이 중학교에 올라와서 헤매는 이유는 뭘까요? 그건 초등수학과 중등수학을 공부할 때 사용하는 머리가 달라서입니다. 초등수학은 ‘2+3=5’와 같이 구체물이나 숫자를 이용해 직관적으로 풀 수 있기 때문에 우뇌를 주로 사용하고, 중학수학은 ‘x+y=5’와 같이 미지수나 문자를 이용해 추상적이고 논리적으로 사고해야 하기 때문에 좌뇌를 주로 사용합니다. 인지발달 관점에서 보면 사람은 초등학교 저학년까지 주로 우뇌를 사용하다, 아홉 살부터 열세 살까지 좌뇌가 단계적으로 성장하는 프로그램을 가지고 있습니다. 그런데 이 시기에 좌뇌 훈련이 충분히 이뤄지지 않으면 좌뇌로 사고하는 중학수학을 맞닥트렸을 때 어려움을 겪게 됩니다.
2. 반복학습으로 중학수학에 필요한 뇌를 만들어라. 어떻게 하면 중학수학을 공부하는 데 필요한 고성능 좌뇌를 얻을 수 있을까요? 이두박근을 단련하려면 아령을 들고 팔을 굽히는 동작을 정확하게 주기적으로 반복해야 하는 것처럼, 좌뇌를 단련하려면 수학적 개념을 ‘반복’해서 문제에 적용하는 연습을 꾸준히 해야 합니다. ‘학습(學習)’이라는 단어의 한자어를 살펴보면 배울 학(學), 익힐 습(習), 즉 어떤 지식을 배우는 것에 그치지 않고 이것이 익숙해질 때까지 연습하라는 뜻이 담겨 있습니다. 불완전한 지식을 완전한 지식으로 만들기 위해서는 반복적으로 연습하거나 실전에 활용해 보는 것이 최고의 방법입니다.
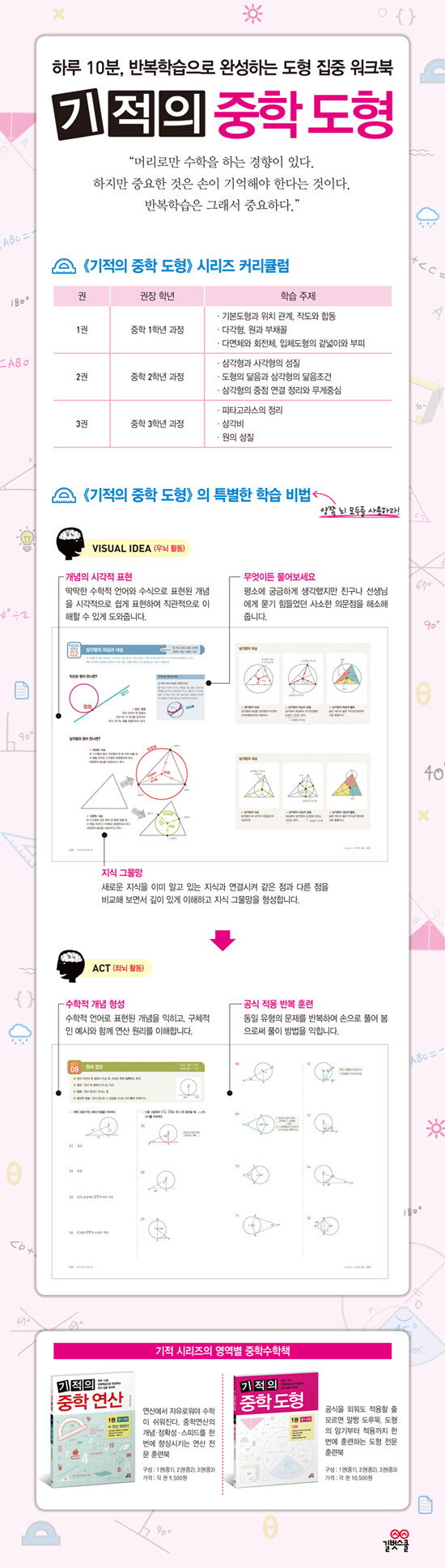
3. 가장 쉽지만, 가장 효과적인 <기적 시리즈>의 반복학습법! 반복이 중요한 건 알겠는데 어떻게 해야 효과적으로 반복할 수 있을까요? <기적의 중학 연산>과 <기적의 중학 도형>은 좌우뇌를 균형 있게 사용하여 더 쉽고, 더 효과적으로 반복할 수 있게 구성되어 있습니다.
는 이미지와 직관을 통한 우뇌 활동으로서 본 학습의 이해를 돕는 보조적인 역할을 하고, 는 추상적이고 논리적인 좌뇌 활동으로서 개념을 문제에 반복해서 적용하는 훈련을 합니다. 기적의 계산법 연구회는 공부하는 방법을 몰라서 우왕좌왕하며 비효율적인 학습 방법에 좌절한 학생들이 쉽고 재미있게 수학을 정복할 수 있도록 가장 쉽고 가장 효과적인 반복학습을 설계했습니다.
4. 이제 중학수학도 영역별로 공부한다.
사람들은 저마다 강점과 약점이 있습니다. 어떤 사람은 연산이 느리거나 정확도가 떨어져 학교 시험을 망치기 일 수이고, 또 다른 사람은 도형 그림을 아무리 들여다봐도 적용할 공식이 떠오르지 않습니다. <기적의 중학 연산>과 <기적의 중학 도형>으로 영역별 기초를 단단히 다지고 응용 학습에 들어가 보세요. 미래의 약점을 예방하고, 현재의 약점을 치료하는 것이 상위권 도약의 첫걸음입니다.
<기적의 중학 연산> 이런 학생들에게 추천합니다.
① 수.연산.방정식 영역의 기초를 탄탄히 다지고 싶은 학생
② 연산 속도가 느려 시험 시간마다 시간이 부족한 학생
③ 잦은 연산 실수로 아깝게 틀리는 문제가 많은 학생
<기적의 중학 도형> 이런 학생들에게 추천합니다.
① 기하 영역의 기초를 탄탄히 다지고 싶은 학생
② 개념과 공식이 이해도 안 되고 외워지지도 않는 학생
③ 개념과 공식을 외웠으나 문제에 적용하지 못하는 학생
작가 소개
저자 : 기적의 계산법 연구회
본 연구회는 아이들이 혼자서 큰 산까지 넘을 수 있는 힘을 키워주고자 합니다. 아이들의 연령에 맞게 학습의 산을 작게 만들어 혼자서 넘을 수 있게 만듭니다. 때로는 작은 고난도 경험하게 하여 작은 성취를 느끼게 합니다. 그리고 아이들에게 실제로 적용해서 검증을 하며 차근차근 책을 출간합니다. 아이가 중심인 기적의 학습법 연구회 [수학 분과]의 대표적 저작물은 <기적의 계산법>, <기적의 도형계산법>, <기적의 중학연산>, <기적의 중학도형>, <기적의 유아계산법> 등이 있습니다.
목차
ACT 01 피타고라스의 정리 1
ACT 02 피타고라스의 정리 2
ACT 03 피타고라스의 정리 이해 1-피타고라스
ACT 04 피타고라스의 정리 이해 2-유클리드
ACT 05 피타고라스의 정리 이해 3-바스카라
ACT 06 피타고라스의 정리와 도형 1
ACT 07 피타고라스의 정리와 도형 2
ACT 08 피타고라스의 정리와 도형 3
ACT 09 피타고라스의 정리와 도형 4
ACT 10 평면도형에서 피타고라스의 정리 활용 1
ACT 11 평면도형에서 피타고라스의 정리 활용 2
ACT 12 평면도형에서 피타고라스의 정리 활용 3
ACT 13 평면도형에서 피타고라스의 정리 활용 4
ACT 14 평면도형에서 피타고라스의 정리 활용 5
ACT 15 입체도형에서 피타고라스의 정리 활용 1
ACT 16 입체도형에서 피타고라스의 정리 활용 2
ACT 17 입체도형에서 피타고라스의 정리 활용 3
ACT 18 입체도형에서 피타고라스의 정리 활용 4
ACT 19 삼각비 1
ACT 20 삼각비 2
ACT 21 삼각비 3
ACT 22 삼각비 4
ACT 23 특수각의 삼각비의 값 1
ACT 24 특수각의 삼각비의 값 2
ACT 25 임의의 예각의 삼각비의 값
ACT 26 삼각비의 표
ACT 27 삼각비 활용 1
ACT 28 삼각비 활용 2
ACT 29 삼각비 활용 3
ACT 30 삼각비 활용 4
ACT 31 삼각비 활용 5
ACT 32 중심각의 크기와 현과 호의 길이
ACT 33 원의 중심과 수직이등분선
ACT 34 현의 길이
ACT 35 원의 접선의 길이
ACT 36 삼각형의 내접원
ACT 37 외접사각형의 성질
ACT 38 원주각과 중심각의 크기
ACT 39 원주각의 성질
ACT 40 원주각의 크기와 호의 길이
ACT 41 네 점이 한 원 위에 있을 조건
ACT 42 원에 내접하는 사각형
ACT 43 원에 내접하는 사각형 활용
ACT 44 접선과 현이 이루는 각
ACT 45 접선과 현이 이루는 각 활용
ACT 46 원에서의 비례 관계
ACT 47 원에서의 비례 관계 활용
ACT 48 네 점이 한 원 위에 있을 조건
ACT 49 할선과 접선의 관계
ACT 50 할선과 접선의 관계 활용

